Algoritmo Page Rank de Google

Contexto y propósito

El contexto empezó al ver el video “Visitiuim cadena de Markov” donde se explica cómo las Cadenas de Markov permitieron a Google convertirse en el mejor buscador del mundo (PageRank): Ver video en YouTube.

A partir de esa inspiración, este proyecto nació como un ejercicio práctico para:

• Aplicar Cadenas de Markov a generación de texto y entender sus limitaciones/fortalezas.
• Consolidar conceptos de álgebra lineal (matrices estocásticas, distribución estacionaria) y el modelo de teletransporte (base de PageRank).
• Disponer de un binario sencillo que entrena una cadena de Markov y genera nuevas secuencias, además de utilidades para experimentar con matrices de transición.

---

Desafíos Técnicos y Soluciones de Ingeniería

1) Tokenización y normalización robustas para español

• Retos:
  • Limpiar puntuación y unificar a minúsculas para evitar explosión del vocabulario.
  • Garantizar un orden determinista del vocabulario para reproducibilidad.
• Solución:
  • La función tokenize convierte a minúsculas, filtra caracteres no alfabéticos (reemplazándolos por espacios) y separa por split_whitespace.
  • El vocabulario se construye con BTreeSet y se vuelca a Vec, lo que asegura orden y, por tanto, índices reproducibles.
• Código clave:
  • src/collections/markov_chain.rs

2) Construcción segura de matrices de transición

• Retos:
  • Evitar estados de matriz inválidos (vacía, no-cuadrada, tamaño 0) y filas con suma 0.
  • Normalizar recuentos a probabilidades fila-a-fila.
• Solución:
  • SquareMatrix::new valida tamaño y forma; SquareMatrix::zeros(n) rechaza n=0.
  • Tras contar bigramas, cada fila se normaliza dividiendo por su suma (si > 0).
• Código clave:
  • src/collections/square_matrix.rs

3) Estrategias de generación: “greedy” no-reflexiva y muestreo ponderado

• Retos:
  • Evitar bucles triviales (quedarse en la misma palabra).
  • Conservar naturalidad alternando entre determinismo y aleatoriedad.
• Solución:
  • next_greedy_nonself elige el siguiente estado con mayor probabilidad excluyendo transiciones a sí mismo; en empate, desempata por índice (determinismo).
  • generate realiza muestreo aleatorio ponderado (con rand) prohibiendo auto-transición; si no hay alternativa, permite cualquiera como “fallback”.
• Código clave:
  • src/collections/markov_chain.rs

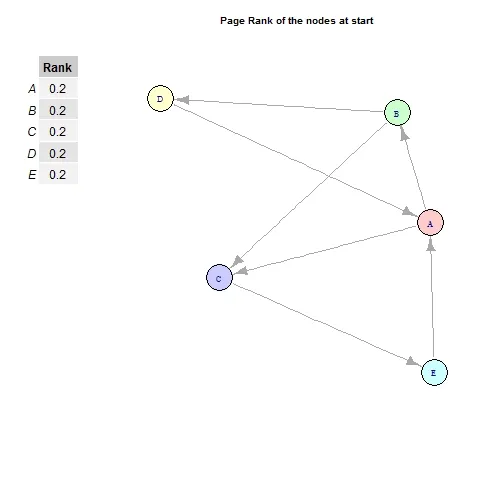
4) PageRank y modelo de teletransporte (eigenvector estacionario)

• Retos:
  • Ilustrar el modelo de teletransporte con factor α (e.g., 0.85) y obtener la distribución estacionaria.
• Solución:
  • Módulo instructions con operaciones de matrices y funciones de ayuda para construir el modelo y calcular el eigenvector dominante.
  • Ejemplo rápido (comentado) en main.rs que muestra: construir matriz, aplicar teletransporte y calcular eigenvector.
• Código clave:
  • src/instructions/matrix_operations.rs
  • src/instructions/markov_chain.rs
  • Demostración en: src/main.rs (bloque comentado al inicio)

---

Organización del Proyecto

• Raíz
  • Cargo.toml (Rust 2024, rand 0.9.x)
  • Cargo.lock
  • .gitignore
  • README.md
• assets/
  • Corpus de ejemplo (p.ej. quijote.txt) para entrenamiento.
• src/
  • main.rs: binario de demostración (generación de texto; ejemplo PageRank comentado).
  • lib.rs: expone módulos de librería.
  • collections/
    • mod.rs
    • square_matrix.rs: tipo SquareMatrix y validaciones.
    • markov_chain.rs: entrenamiento y generación.
  • instructions/
    • mod.rs
    • matrix_operations.rs
    • markov_chain.rs
• docs/
  • Material auxiliar (si procede).
• tests/
  • Espacio para pruebas (WIP).
• .github/
  • Carpeta reservada para flujos de CI/CD (si se añaden).

---

API de librería (ejemplo de uso)

use markov_chain::collections::MarkovChain;

fn main() -> Result<(), Box<dyn std::error::Error>> {
    let texto = "hola hola adios mundo adios hola mundo";
    let mut mc = MarkovChain::new();

    mc.fit(texto)?;
    let greedy = mc.generate_greedy_nonself("hola", 10).unwrap();
    let random = mc.generate("hola", 10).unwrap();

    println!("Greedy: {}", greedy);
    println!("Random: {}", random);
    Ok(())
}

Puntos clave:

• fit(&str): entrena con un corpus en texto plano.
• generate_greedy_nonself(start, pasos): elige siempre la transición más probable (excluyendo auto-transiciones).
• generate(start, pasos): muestreo aleatorio ponderado; evita auto-transiciones si es posible.

---

Cómo funciona (alto nivel)

1. Tokenización:
   • Minúsculas, filtrado de símbolos no alfabéticos y partición por espacios.
2. Vocabulario e índices:
   • Con BTreeSet para orden determinista; mapeo palabra→índice con BTreeMap.
3. Conteo y normalización:
   • Bigrama (w_i → w_{i+1}) incrementa M[i][j].
   • Cada fila se normaliza para que sume 1, formando una matriz estocástica fila.
4. Generación:
   • Greedy no-reflexiva: evita quedarse en el mismo estado; en empate, el más “temprano” por índice.
   • Aleatoria: muestreo proporcional a M[i][*] (con rand); “fallback” si la fila efectiva queda sin masa.
5. PageRank (demo):
   • Construye M_α = αM + (1-α)U (mezcla con distribución uniforme) y obtiene la distribución estacionaria por eigenvector.

---

Limitaciones y mejoras futuras

• Vocabulario a nivel de palabra únicamente (no n-gramas > 2).
• No se preserva puntuación ni mayúsculas originales.
• No se establecen semillas RNG; añadir opción para reproducibilidad total.
• Suavizado (Laplace/Kneser-Ney) para manejar mejor palabras raras.
• Serialización del modelo (guardar/cargar) y exposición como crate en crates.io.
• Tests adicionales en tests/ y benchmarks de rendimiento.

---

Bibliografía

• Video (YouTube): Cadenas de Markov y PageRank
• UGR: Cadenas de Markov
• Google PageRank
• Cadenas de Markov homogéneas